Что такое математический анализ

Введение в математический анализ

Объяснение, что такое математический анализ

Математический анализ — это раздел математики, который помогает нам понимать и изучать, как изменяются числа и функции. Он позволяет нам изучать изменения величин с течением времени и понимать, как они связаны друг с другом.

Цель математического анализа

Главная цель математического анализа — это понимание и описание изменений в математических объектах. Мы используем его, чтобы понять, как меняются значения функций, графики и другие математические объекты.

Примеры задач математического анализа

Важно понимать, что математический анализ используется во многих областях науки и инженерии. Например:

• Когда мы изучаем движение автомобиля, мы можем использовать математический анализ, чтобы выяснить, как меняется его скорость.
• При исследовании изменений температуры с течением времени, мы также можем применять математический анализ.

Важность математического анализа

Математический анализ является одним из ключевых инструментов в науке и инженерии. Он помогает нам делать прогнозы, решать сложные задачи и понимать мир вокруг нас.

Итак, математический анализ — это мощный инструмент, который помогает нам изучать и понимать изменения в числах и функциях. Мы будем исследовать его более подробно, чтобы научиться решать различные задачи и использовать его в реальной жизни.

Основы математического анализа

Разбор понятий, таких как функции, переменные, производные и интегралы

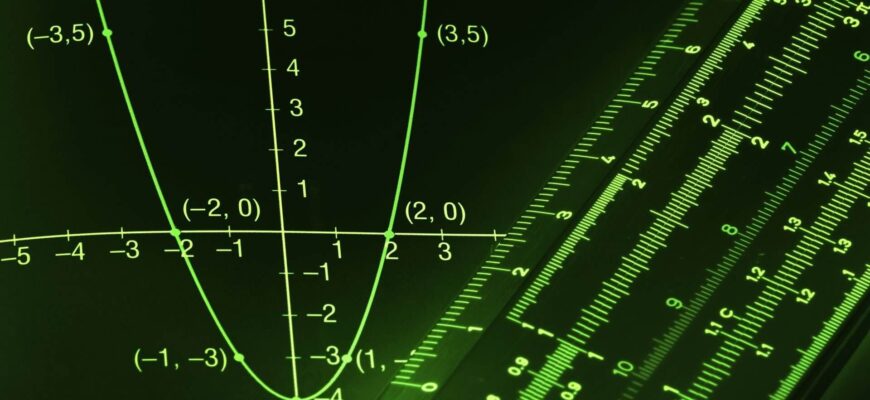
Понятие функции

В математическом анализе, функция — это способ описать зависимость одной величины от другой. Функция принимает на вход одно число (или более) и выдаёт другое число. Например, если у нас есть функция, которая описывает, как меняется температура воздуха от времени, то на вход она принимает время, а на выходе дает температуру.

Переменные и их роль в функциях

В функциях мы используем переменные. Переменные — это символы, которые представляют числа. Например, в функции температуры временем, переменная времени может быть обозначена буквой «t». И таким образом, мы можем записать функцию как «T(t)», где «T» — это температура, а «t» — время.

Производные функций

Производная функции — это показатель, который позволяет нам понять, как быстро функция меняется в данной точке. Если функция представляет график зависимости, то производная показывает наклон этой кривой в данной точке. Если производная положительна, это значит, что функция растет; если отрицательна, то функция убывает.

Интегралы функций

Интеграл функции — это инструмент, который позволяет нам найти площадь под графиком этой функции. Важно понимать, что если у нас есть график функции и мы хотим найти, сколько площади он занимает в каком-то интервале, то интеграл помогает нам это сделать.

Примеры использования производных и интегралов

Давай рассмотрим пример. Если у нас есть график функции, представляющей скорость автомобиля, производная этой функции покажет нам, как быстро меняется скорость в конкретный момент времени. Интеграл этой функции может показать, какое расстояние проехал автомобиль за определенное время.

Объяснение, какие важные вещи можно узнать, изучая эти понятия

Основы математического анализа позволяют нам понимать и изучать изменения величин в различных ситуациях. Это помогает ученым, инженерам и другим профессионалам делать более точные расчеты и прогнозы.

В этом разделе мы изучили основы математического анализа, включая функции, переменные, производные и интегралы. Эти понятия являются ключевыми в изучении изменений в математике и ее применении в реальной жизни.

Производные и их роль в анализе

Объяснение, что такое производная функции

Что такое производная

Производная функции — это способ измерить, насколько быстро эта функция меняется в какой-то конкретной точке. Когда мы рассматриваем график функции, производная в этой точке показывает нам, насколько круто или полого этот график поднимается или опускается.

Геометрическая интерпретация производной

Можно представить себе производную как наклон касательной линии к графику функции в определенной точке. Если производная положительна, то касательная линия будет подниматься вверх; если отрицательна, то опускаться вниз. Чем круче наклон касательной, тем больше значение производной.

Как найти производную

Для большинства функций производная находится с помощью математических правил. Например, для функции «y = x^2» производная будет «2x». Это означает, что скорость изменения функции «y» в любой точке равна удвоенной координате «x» в этой точке.

Примеры использования производных, например, для определения скорости изменения чего-либо

Производные играют огромную роль в решении задач в физике, экономике, инженерии и других науках. Например, если у нас есть график, показывающий, как меняется скорость автомобиля с течением времени, мы можем использовать производную, чтобы узнать, когда автомобиль двигался быстрее или медленнее.

Понимание таргетинга

Давай представим, что у тебя есть рогатка, и ты хочешь попасть в цель. Если ты знаешь, как изменяется положение мишени относительно времени, то производная покажет тебе, какой угол наклона рогатки нужен, чтобы попасть в цель.

Значение производных в научных исследованиях

Ученые используют производные для изучения изменений в природе и создания моделей. Например, в физике производные помогают понимать движение планет и частиц, а в экономике — предсказывать рост и падение цен.

Вывод

Производные — это мощный инструмент, который позволяет нам изучать и понимать изменения в функциях и графиках. Они играют важную роль в различных областях науки и практических приложениях, помогая нам делать более точные расчеты и принимать более информированные решения.

Интегралы и их применение

Объяснение, что такое интеграл функции

Интеграл — это математический инструмент, который позволяет нам находить площадь под графиком функции или суммировать бесконечно маленькие изменения величины в течение определенного интервала.

Геометрическая интерпретация интеграла

Можно представить себе интеграл как способ нахождения площади между графиком функции и горизонтальной осью. Если функция представляет собой кривую, то интеграл покажет, какая площадь ограничена этой кривой.

Определенный и неопределенный интеграл

Существуют два основных типа интегралов. Неопределенный интеграл, или первообразная, находит функцию, производная которой равна данной функции. Определенный интеграл, с другой стороны, находит числовое значение площади между графиком функции и осью абсцисс в определенном интервале.

Примеры использования интегралов, например, для вычисления площадей или объемов

Интегралы играют важную роль в различных областях. Например, в физике, они используются для расчета пути, который прошел объект с изменяющейся скоростью. В экономике, интегралы могут помочь определить общую стоимость производства товаров.

Понимание площади под кривой

Давай представим, что у нас есть график функции, представляющей скорость автомобиля в течение определенного времени. Интеграл этой функции в определенном интервале даст нам полный путь, который проехал автомобиль за это время.

Роль интегралов в научных исследованиях

Ученые используют интегралы для анализа данных и построения моделей. Например, в биологии, интегралы могут помочь определить общее количество популяции живых существ в определенной области.

Интегралы — это мощный инструмент, который позволяет нам находить площади, суммировать изменения и анализировать данные. Они имеют множество практических применений в различных областях, помогая нам понимать и описывать мир вокруг нас и решать разнообразные задачи.

Практические примеры и применение математического анализа

Математический анализ является неотъемлемой частью различных научных и инженерных областей, а также применяется в повседневной жизни. Давай рассмотрим несколько конкретных примеров его практического использования.

Прогноз погоды

Метеорологи используют математический анализ для создания моделей, которые предсказывают погоду. Они анализируют данные о температуре, влажности, давлении и ветре, чтобы делать прогнозы о том, как изменится погода в будущем.

Дизайн инженерных систем

Инженеры используют математический анализ при проектировании различных систем, таких как мосты, здания, электронные устройства и многое другое. Они рассчитывают, как будут взаимодействовать разные элементы системы и как они будут работать в разных условиях.

Физические законы

Физики используют математический анализ для описания и предсказания физических явлений, таких как движение тел, распространение света и электромагнитные волны. Уравнения, основанные на математическом анализе, помогают нам понимать природу и взаимодействие вещей во вселенной.

Медицинская диагностика

В медицине математический анализ используется для обработки медицинских данных, например, для анализа изображений, определения характеристик пациентов и предсказания заболеваний. Это помогает врачам принимать более точные диагнозы и рекомендовать наилучшее лечение.

Экономический анализ

Экономисты используют математический анализ для изучения экономических явлений, таких как рост ВВП, инфляция и рыночные цены. Математические модели помогают им понимать и прогнозировать поведение рынков и экономических систем.

Космические исследования

В астрономии и астрофизике математический анализ играет важную роль в исследовании космоса. Ученые используют математические модели для предсказания движения планет, галактик и других астрономических объектов.

Математический анализ — это мощный инструмент, который применяется во многих областях науки и инженерии. Он помогает нам понимать и описывать изменения в мире, решать сложные задачи и делать нашу жизнь лучше и безопаснее. Важно учиться и понимать его, так как он может быть полезен в различных аспектах нашей жизни.

Подробное видео про математический анализ от доктора физико-математических наук