- Основные тригонометрические функции
- Введение в синус, косинус и тангенс
- Определение и значения функций в различных угловых единицах
- Графики синусоид и их основные характеристики
- Основные тригонометрические тождества
- Тождества прямоугольного треугольника
- Тождества суммы углов
- Тождества двойного угла
- Тождества половинного угла
- Применение тригонометрических тождеств для упрощения выражений и решения уравнений
- Вывод
- Тригонометрические функции
- Периодичность и графики тригонометрических функций
- Периодичность синуса и косинуса
- Графики тригонометрических функций
- Периоды и фазовые сдвиги
- Вывод
- Формулы тригонометрии суммы и разности
- Формулы тригонометрии для суммы и разности синусов
- Применение этих формул для нахождения значений тригонометрических функций в разных углах
- Практические примеры использования формул суммы и разности
- Видео про основные формулы тригонометрии
Основные тригонометрические функции
Формулы тригонометрии являются одними из самых важных в математике. Они используются в различных областях, таких как физика, инженерия, архитектура и другие. Для начала рассмотрим основные тригонометрические функции: синус, косинус и тангенс, их определение и значения в различных угловых единицах, а также графики синусоид и их основные характеристики.
Введение в синус, косинус и тангенс
Синус, косинус и тангенс являются тригонометрическими функциями, которые используются для вычисления отношений сторон прямоугольного треугольника. Они определяются как отношения длин сторон треугольника к его углам.
Синус угла определяется как отношение противолежащей стороны к гипотенузе треугольника. Косинус угла определяется как отношение прилежащей стороны к гипотенузе треугольника. Тангенс угла определяется как отношение противолежащей стороны к прилежащей стороне треугольника.
Определение и значения функций в различных угловых единицах
Тригонометрические функции могут быть выражены в различных угловых единицах, таких как радианы и градусы. Радианы являются наиболее распространенной угловой единицей в математике, а градусы используются в повседневной жизни.
Значения синуса, косинуса и тангенса угла могут быть вычислены с помощью таблиц и калькуляторов. Например, синус угла 30 градусов равен 0.5, а косинус угла 45 градусов равен 0.707.
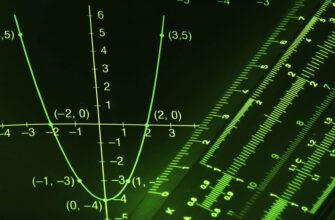
Графики синусоид и их основные характеристики
График синусоиды представляет собой график синуса функции от угла. Он имеет форму волны и периодически повторяется. График косинуса имеет такую же форму, но смещен на 90 градусов.
Основные характеристики графика синусоиды включают амплитуду, период и фазу. Амплитуда представляет собой максимальное значение функции, период — расстояние между двумя соседними пиками или минимумами, а фаза — смещение графика влево или вправо.
Основные тригонометрические тождества
Тригонометрические тождества — это формулы, которые связывают тригонометрические функции углов между собой. Они являются основой тригонометрии и широко используются в математике, физике, инженерии и других науках. В этом ответе мы рассмотрим основные тригонометрические тождества и их применение для упрощения выражений и решения уравнений.
Тождества прямоугольного треугольника
В прямоугольном треугольнике со сторонами a, b и гипотенузой c, где угол между сторонами a и b равен α, справедливы следующие тригонометрические тождества:
- $\sin\alpha = \frac{a}{c}$
- $\cos\alpha = \frac{b}{c}$
- $\tan\alpha = \frac{a}{b}$
- $\cot\alpha = \frac{b}{a}$
- $\sec\alpha = \frac{c}{b}$
- $\csc\alpha = \frac{c}{a}$
Тождества суммы углов
Тригонометрические тождества суммы углов связывают тригонометрические функции суммы углов с тригонометрическими функциями отдельных углов. Некоторые из них:
- $\sin(\alpha + \beta) = \sin\alpha\cos\beta + \cos\alpha\sin\beta$
- $\cos(\alpha + \beta) = \cos\alpha\cos\beta — \sin\alpha\sin\beta$
- $\tan(\alpha + \beta) = \frac{\tan\alpha + \tan\beta}{1 — \tan\alpha\tan\beta}$
Тождества двойного угла
Тригонометрические тождества двойного угла связывают тригонометрические функции двойного угла с тригонометрическими функциями отдельного угла. Некоторые из них:
- $\sin(2\alpha) = 2\sin\alpha\cos\alpha$
- $\cos(2\alpha) = \cos^2\alpha — \sin^2\alpha$
- $\tan(2\alpha) = \frac{2\tan\alpha}{1 — \tan^2\alpha}$
Тождества половинного угла
Тригонометрические тождества половинного угла связывают тригонометрические функции половинного угла с тригонометрическими функциями отдельного угла. Некоторые из них:
- $\sin\left(\frac{\alpha}{2}\right) = \pm\sqrt{\frac{1 — \cos\alpha}{2}}$
- $\cos\left(\frac{\alpha}{2}\right) = \pm\sqrt{\frac{1 + \cos\alpha}{2}}$
- $\tan\left(\frac{\alpha}{2}\right) = \pm\sqrt{\frac{1 — \cos\alpha}{1 + \cos\alpha}}$
Применение тригонометрических тождеств для упрощения выражений и решения уравнений
Тригонометрические тождества могут быть использованы для упрощения сложных тригонометрических выражений. Например, если нужно упростить выражение $\sin^2\alpha + \cos^2\alpha$, то можно использовать тождество $\sin^2\alpha + \cos^2\alpha = 1$.Тригонометрические тождества также могут быть использованы для решения тригонометрических уравнений. Например, если нужно решить уравнение $\sin\alpha = \frac{1}{2}$, то можно использовать тождество $\sin\alpha = \sin\beta \Rightarrow \alpha = n\pi + (-1)^n\beta$, где n — целое число, а $\beta$ — угол, для которого $\sin\beta = \frac{1}{2}$. В данном случае, $\beta = \frac{\pi}{6}$, поэтому $\alpha = n\pi + (-1)^n\frac{\pi}{6}$.
Вывод
Тригонометрические тождества — это важный инструмент в тригонометрии, который позволяет связывать тригонометрические функции углов между собой. Они могут быть использованы для упрощения выражений и решения уравнений. Знание основных тригонометрических тождеств является необходимым для понимания более сложных тригонометрических концепций и их применения в науке и технике.
Тригонометрические функции
Тригонометрические функции — это функции, которые используются для описания отношений между сторонами и углами в треугольниках. Они широко используются в математике, физике, инженерии и других науках. Формулы тригонометрии используются для вычисления значений тригонометрических функций для различных углов.Значения тригонометрических функций для 30, 45 и 60 градусов (или π/6, π/4 и π/3 радиан) являются особыми и широко используются в различных задачах. Ниже приведены значения тригонометрических функций для этих углов:
| Угол | Синус | Косинус | Тангенс | Котангенс | Секанс | Косеканс |
|---|---|---|---|---|---|---|
| 30° | 1/2 | √3/2 | 1/√3 | √3 | 2 | 2/√3 |
| 45° | √2/2 | √2/2 | 1 | 1 | √2 | √2 |
| 60° | √3/2 | 1/2 | √3 | 1/√3 | 2/√3 | 2 |
| π/6 | 1/2 | √3/2 | 1/√3 | √3 | 2 | 2/√3 |
| π/4 | √2/2 | √2/2 | 1 | 1 | √2 | √2 |
| π/3 | √3/2 | 1/2 | √3 | 1/√3 | 2/√3 | 2 |
Применение этих значений в различных задачах:
- Решение треугольников: значения тригонометрических функций для специальных углов используются для решения треугольников, когда известны две стороны и угол между ними.
- Расчет высоты и длины биссектрисы треугольника: значения тригонометрических функций для специальных углов используются для расчета высоты и длины биссектрисы треугольника.
- Расчет периода и частоты колебаний: значения тригонометрических функций для специальных углов используются для расчета периода и частоты колебаний в физике и инженерии.
- Расчет углов наклона: значения тригонометрических функций для специальных углов используются для расчета углов наклона в геометрии и строительстве.
В заключение, значения тригонометрических функций для специальных углов (30, 45 и 60 градусов или π/6, π/4 и π/3 радиан) являются особыми и широко используются в различных задачах. Формулы тригонометрии используются для вычисления значений тригонометрических функций для различных углов, что позволяет решать различные задачи в математике, физике, инженерии и других науках.
Периодичность и графики тригонометрических функций
Периодичность синуса и косинуса
- Синус и косинус являются периодическими функциями, то есть они повторяются через определенные интервалы времени или расстояния.
- Период синуса и косинуса равен 2π, что означает, что функция повторяется каждые 2π единиц времени или расстояния.
- Формулы тригонометрии, такие как sin(x + 2π) = sin(x) и cos(x + 2π) = cos(x), подтверждают периодичность синуса и косинуса.
Графики тригонометрических функций
- График синуса и косинуса представляет собой периодическую кривую, которая колеблется между значениями -1 и 1.
- Амплитуда синуса и косинуса равна 1, что означает, что колебания функции находятся в пределах от -1 до 1.
- Смещение синуса и косинуса определяет, насколько функция сдвинута вправо или влево от начала координат. Например, sin(x — π/2) имеет смещение вправо на π/2 единиц.
Периоды и фазовые сдвиги
- Период тригонометрической функции определяет, через какие интервалы времени или расстояния функция повторяется.
- Фазовый сдвиг определяет, насколько функция сдвинута вправо или влево от начала координат.
- Формулы тригонометрии, такие как sin(x + π) = -sin(x) и cos(x + π) = -cos(x), показывают, как изменяется функция при фазовом сдвиге на π единиц.
- Формулы тригонометрии также могут использоваться для нахождения периодов и фазовых сдвигов тригонометрических функций.
Вывод
Тригонометрические функции, такие как синус и косинус, являются периодическими функциями, которые повторяются через определенные интервалы времени или расстояния. Графики тригонометрических функций представляют собой периодические кривые, которые колеблются между значениями -1 и 1. Амплитуда и смещение тригонометрических функций могут изменяться, но период всегда равен 2π. Формулы тригонометрии могут использоваться для нахождения периодов и фазовых сдвигов тригонометрических функций.
Формулы тригонометрии суммы и разности
Формулы тригонометрии для суммы и разности синусов
Формулы для суммы и разности синусов и косинусов являются важными инструментами в тригонометрии и могут быть полезными при решении различных задач. Давайте рассмотрим их подробнее.
Формулы суммы синусов и косинусов:
Формула суммы синусов
sin(A+B)=sin(A)cos(B)+cos(A)sin(B)
Эта формула позволяет выразить синус суммы двух углов через синус и косинус каждого из углов.
Формула суммы косинусов
cos(A+B)=cos(A)cos(B)−sin(A)sin(B)
Эта формула позволяет выразить косинус суммы двух углов через косинус и синус каждого из углов.
Формулы разности синусов и косинусов:
Формула разности синусов
sin(A−B)=sin(A)cos(B)−cos(A)sin(B)
Эта формула позволяет выразить синус разности двух углов через синус и косинус каждого из углов.
Формула разности косинусов
cos(A−B)=cos(A)cos(B)+sin(A)sin(B)
Эта формула позволяет выразить косинус разности двух углов через косинус и синус каждого из углов.
Применение этих формул для нахождения значений тригонометрических функций в разных углах
Формулы суммы и разности синусов и косинусов играют важную роль в тригонометрии и позволяют находить значения тригонометрических функций в различных углах. Они широко используются для:
- Нахождения значений синуса и косинуса суммы и разности углов: эти формулы позволяют выразить синус и косинус суммы (или разности) двух углов через синусы и косинусы этих углов, что полезно при решении сложных задач.
- Решения тригонометрических уравнений: формулы суммы и разности позволяют упростить уравнения и находить значения углов, удовлетворяющих заданным условиям.
- Работы с графиками тригонометрических функций: зная формулы для суммы и разности синусов и косинусов, можно анализировать и изменять графики этих функций при разных углах.
Практические примеры использования формул суммы и разности
- Механика: формулы тригонометрии применяются в механике для анализа движения объектов с переменной скоростью и ускорением. Например, при баллистическом движении тела под углом к горизонту, формулы суммы и разности позволяют вычислять компоненты скорости и ускорения в направлении движения и перпендикулярно к нему.
- Электроника и инженерия: в электронике и инженерии формулы суммы и разности синусов и косинусов применяются для анализа переменных сигналов, фазовой модуляции, аналоговой и цифровой обработки сигналов.
- Архитектура и строительство: в строительстве и архитектуре формулы суммы и разности используются для решения задач, связанных с расчетами углов наклона крыш, вычисления расстояний и высот, определения угловых отклонений и т. д.
Формулы тригонометрии для суммы и разности синусов и косинусов существенны во многих областях науки и инженерии, и их понимание является ключевым для решения разнообразных практических задач.